【主要内容】导数、导函数、左(右)导数、微分和高阶导数的定义。导数与微分的关系、导数四则运算、复合运算法则、导数及微分的几何意义。
【常用方法】利用左、右导数概念;复合求导法则;对数求导法;利用一阶微分不变性求导。
【典型例题】
【例1】设函数

在

内有界且可导,则( )
(A) 当

时,必有

;
(B) 当

存在时,必有

;
(C) 当

时,必有

;
(D) 当

存在时,必有

;
【分析】考查导数的概念及极限的含义
【答案】B
【例2】函数
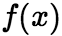
在
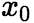
点可导的一个充分条件是
(A)

存在;
(B)

存在;
(C)

存在;
(D)

存在。
【分析】考查导数的定义,导数的判断
【答案】D
【例3】设

,且导数存在,则

( )
(A)0



【分析】利用导数的定义求极限
【答案】D
【例4】求函数

,其中
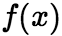
具有连续的导数,且

。(1)确定

使得

连续;(2)研究

的连续性。
【分析】考查分段函数的连续性和可导性
【例5】函数

在点x=1可导,求 的值
(A)a=2,b=1 (B)a=1,b=2
(C)a=2,b=-1 (D)a=-1,b=2
【分析】分段函数在分段点处的可导性
【答案】C
【例6】已知曲线

与

在点

处的切线相同,写出切线方程,并求极限
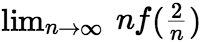
。
【分析】考查导数的几何意义,极限
【答案】切线方程:y=x;

【例7】曲线

在点(1,1)处的切线为( )
(A)x+y=-2 (B)x+y=2 (C)x-y=2 (D)x-y=-2
【分析】导数的几何意义,求切线方程
【答案】B
【例8】已知
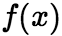
是周期为5的连续函数,它在
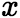
=0的某邻域内满足关系式

其中

是比
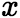
高阶的无穷小,且
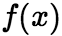
在
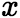
=1处可导,求曲线

在

处的切线方程.
【分析】考查周期函数,导数的定义及切线方程
【答案】切线方程:

【例9】设
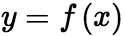
在x=1处连续且周期为2的周期函数,

,则曲线
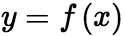
过点(-1,f(-1))的切线方程为( )
(A)y=2(x-1) (B)y=2(x+1)
(C)y=x-1 (D)y=2x-1
【分析】周期函数,导数定义,切线方程
【答案】B
 在
在 内有界且可导,则( )
(A) 当
内有界且可导,则( )
(A) 当 时,必有
时,必有 ;
(B) 当
;
(B) 当 存在时,必有
存在时,必有 ;
(C) 当
;
(C) 当 时,必有
时,必有 ;
(D) 当
;
(D) 当 存在时,必有
存在时,必有 ;
【分析】考查导数的概念及极限的含义
【答案】B
【例2】函数
;
【分析】考查导数的概念及极限的含义
【答案】B
【例2】函数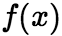 在
在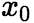 点可导的一个充分条件是
(A)
点可导的一个充分条件是
(A) 存在;
(B)
存在;
(B)  存在;
(C)
存在;
(C)  存在;
(D)
存在;
(D) 存在。
【分析】考查导数的定义,导数的判断
【答案】D
【例3】设
存在。
【分析】考查导数的定义,导数的判断
【答案】D
【例3】设 ,且导数存在,则
,且导数存在,则 ( )
(A)0
( )
(A)0 

 【分析】利用导数的定义求极限
【答案】D
【例4】求函数
【分析】利用导数的定义求极限
【答案】D
【例4】求函数 ,其中
,其中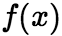 具有连续的导数,且
具有连续的导数,且 。(1)确定
。(1)确定 使得
使得 连续;(2)研究
连续;(2)研究 的连续性。
【分析】考查分段函数的连续性和可导性
【例5】函数
的连续性。
【分析】考查分段函数的连续性和可导性
【例5】函数 在点x=1可导,求 的值
(A)a=2,b=1 (B)a=1,b=2
(C)a=2,b=-1 (D)a=-1,b=2
【分析】分段函数在分段点处的可导性
【答案】C
【例6】已知曲线
在点x=1可导,求 的值
(A)a=2,b=1 (B)a=1,b=2
(C)a=2,b=-1 (D)a=-1,b=2
【分析】分段函数在分段点处的可导性
【答案】C
【例6】已知曲线 与
与 在点
在点 处的切线相同,写出切线方程,并求极限
处的切线相同,写出切线方程,并求极限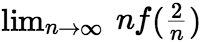 。
【分析】考查导数的几何意义,极限
【答案】切线方程:y=x;
。
【分析】考查导数的几何意义,极限
【答案】切线方程:y=x; 【例7】曲线
【例7】曲线 在点(1,1)处的切线为( )
(A)x+y=-2 (B)x+y=2 (C)x-y=2 (D)x-y=-2
【分析】导数的几何意义,求切线方程
【答案】B
【例8】已知
在点(1,1)处的切线为( )
(A)x+y=-2 (B)x+y=2 (C)x-y=2 (D)x-y=-2
【分析】导数的几何意义,求切线方程
【答案】B
【例8】已知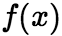 是周期为5的连续函数,它在
是周期为5的连续函数,它在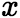 =0的某邻域内满足关系式
=0的某邻域内满足关系式
 其中
其中 是比
是比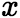 高阶的无穷小,且
高阶的无穷小,且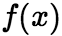 在
在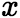 =1处可导,求曲线
=1处可导,求曲线 在
在 处的切线方程.
【分析】考查周期函数,导数的定义及切线方程
【答案】切线方程:
处的切线方程.
【分析】考查周期函数,导数的定义及切线方程
【答案】切线方程: 【例9】设
【例9】设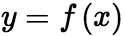 在x=1处连续且周期为2的周期函数,
在x=1处连续且周期为2的周期函数, ,则曲线
,则曲线 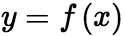 过点(-1,f(-1))的切线方程为( )
(A)y=2(x-1) (B)y=2(x+1)
(C)y=x-1 (D)y=2x-1
【分析】周期函数,导数定义,切线方程
【答案】B
过点(-1,f(-1))的切线方程为( )
(A)y=2(x-1) (B)y=2(x+1)
(C)y=x-1 (D)y=2x-1
【分析】周期函数,导数定义,切线方程
【答案】B